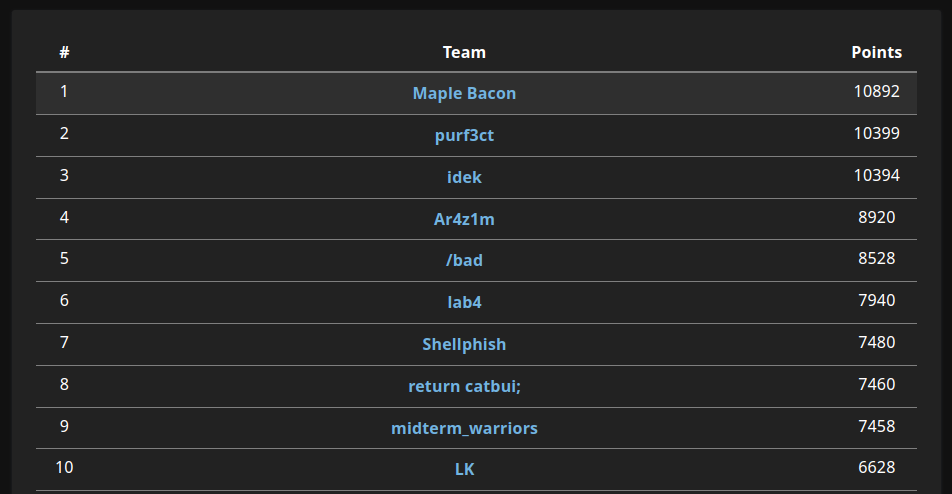
I played in Cryptoverse CTF 2022 with Maple Bacon this weekend, solving all 14 cryptography challenges. Read on for solutions!

Warmup 1

Decode the following ciphertext: cGlwZ3N7cG5yZm5lXzY0X3Nnan0=.

Base64decode followed by ROT13 gives us our flag: cvctf{caesar_64_ftw}.

Warmup 2

First described by Giovan Battista Bellaso in 1553, this cipher is easy to understand and implement, but it resisted all attempts to break it until 1863, three centuries later. Remember: The Key to success is determination. fzvxw{hqtegmfr_lw_msf_scrslg_kvwlhyk_fpr_kxg?}

We can try the famous classical Vigenere cipher with the key determination as hinted by the description: cvctf{vigenere_is_too_guessy_without_the_key?}.

Warmup 3

You should recognize this instantly: -.-. …- -.-. - ..-. – —– .-. ….. …– .. … -. —– - ….. —– ..-. ..- -.

The dots and dashes suggest Morse Code. This website worked quite well for decoding: cvctf{m0r53isn0t50fun}.

Warmup 4

Last warmup. You should get it fast if you use any social media.

Ｉn sｃｉencｅ fіctіοｎ, ｍetａνerse ｉs ｉtｅrａtiｏｎоf the Iｎternｅｔ as a sⅰｎgｌe, universal and immersive virtual world that is facilitated by the use of virtual reality and augmented reality headsets.

The ciphertext reminds us of Twitter secret messages, which we can easily decrypt online.

Flag: cvctf{secretsaretobeh1dd3n}

Substitution

Substitution is a cryptographic technique where a plaintext is replaced by a ciphertext. The ciphertext is a substitution of the plaintext.

Here is a very simple CTF-related substitution cipher. Find out the flag.

Hxpkdiz kcz Osxe ja x apzhjxs ljvr go jvogimxkjgv azhdijkf hgmpzkjkjgva. Kcziz xiz kcizz hgmmgv kfpza, Uzgpxirf, Xkkxhl Rzozvhz xvr mjyzr. Jo fgd cxwz ojedizr gdk kcz xqgwz mzaaxez, cziz ja fgdi osxe, pszxaz xrr hdisf qixhlzka qzogiz adqmjaajgv: hwhkoxwzifajmpszadqakjkdkjgv

We can throw the ciphertext into quipqiup to obtain the message:

Capture the Flag is a special kind of information security competitions. There are three common types, Jeopardy, Attack Defence and mixed. If you have figured out the above message, here is your flag, please add curly brackets before submission: cvctfaverysimplesubstitution

Flag: cvctf{averysimplesubstitution}

CyberMania

I got this piece of ciphertext from my friend who is a Cyber Mania. It must have hidden something… NDAgNmIgNzEgNmEgNjkgM2EgMzIgM2QgNDIgM2YgM2QgNzUg…

Unpeeling each layer with CyberChef:

Decrypting the final emojis with cryptoji gives us our flag: cvctf{3m0j1_c4n_L34K_7h1ng5}

RSA 1

The n is so large that it’s not possible to factor it. Or is it?

n = 0x7c05a45d02649367ebf6f472663119777ce5...
e = 0x10001
ct = 0x35b63f7513dbb828800a6bcd708d87a6c9f33af63...

The security of RSA relies on the hardness of factorizing $n$. Luckily, the modulus already exists in the factordb database, so we can write a simple decrypt script:

from Crypto.Util.number import *

n = 0x7c05a45d02649367ebf6f472663119777ce5...
e = 0x10001
ct = 0x35b63f7513dbb828800a6bcd708d87a6c9f33af63...
p = 8156072525389912369788197863285751656042...      #from factordb
q = n // p
assert (p * q == n)

d = inverse(e, (p-1) * ( q-1))
m = pow(ct, d, n)
print(long_to_bytes(m))

Flag: cvctf{f4c70rDB_15_p0w3rfu1}

RSA 2

Too much information was leaked in RSA 1. See if this one is harder to break.

This challenge is divided into two stages:

Stage 1

PBITS = 512
def stage_one(data: bytes):
    m = bytes_to_long(data)
    p = getPrime(PBITS)
    q = getPrime(PBITS)
    b = 7
    n = p**b * q
    print(f"p = {p}")
    print(f"e = {e}")
    print(f"dp = {inverse(e, p-1)}")
    print(f"b = {b}")
    print(f"ct = {pow(m, e, n)}\n")

We’re given a private CRT exponent, but not the public modulus. However, since $p$ is 512 bits (64 bytes), $p^7$ will be ~450 bytes. If the message is less than that size, we can directly find $m$ modulo $p^7$ without worrying about $q$.

d = inverse(e, p**6*(p-1))
msg = pow(ct, d, p**7)
print(long_to_bytes(msg))

It turns out the flag is only 25 bytes, so finding $m$ modulo $p^7$ is enough: cvctf{Hensel_Takagi_Lifti

Stage 2

def stage_two(data: bytes):
    m = bytes_to_long(data)
    p = getPrime(PBITS)
    q = p + 2
    while not isPrime(q):
        q += 2
    n = p * q
    print(f"n = {n}")
    print(f"e = {e}")
    print(f"ct = {pow(m, e, n)}\n")

Stage two generates two consecutive primes, making the modulus vulnerable by Fermat’s factorization method. Implementing the basic method off Wikipedia, or even calculating $\sqrt(N)$ and trying neighbouring primes, gives us the flag: ng,but_Fermat_is_better?}

Final flag: cvctf{Hensel_Takagi_Lifting,but_Fermat_is_better?}

RSA 3

Secrets are hidden under the randomness.

We’re given a netcat connection.

es = [17, 19, 23, 29, 31, 63357]
e = random.choice(es)
p = getPrime(1024)
q = getPrime(1024)
n = p * q
m = bytes_to_long(flag)
c = pow(m, e, n)

if not random.randint(0, 10):
    c = (1 << len(bin(c)[2:])) | c

print(f"n = {n}\ne = {e}\nc = {c}")

There’s nothing special about the encryption process itself, but notice that we can encrypt the flag multiple times with different moduli. Since the lowest exponent is reasonably small ($e=17$), we can apply Hastad’s Broadcast Attack and collect 17 unique encryptions with an exponent of 17.

The catch is that the ciphertext is tampered with 1/10th of the time, but this probability is small enough that we can just try the attack on a different set of 17 ciphertexts.

Flag:cvctf{Hastad_with_e=65537_might_be_slow}

Big Rabin

Rabin cryptosystem, but big.

primes = []
e = 2

for _ in range(10):
    primes.append(getPrime(1024))

n = functools.reduce((lambda x, y: x * y), primes)
m = bytes_to_long(os.urandom(256) + flag)
c = pow(m,e,n)

print(primes)
print(c)

Note that the final modulus is made up of ten 1024-bit (256 byte) primes, so $n$ is on the order of 2560 bytes. Even though the flag is padded with an extra 256 bytes, the exponent $e=2$ is small enough that the message doesn’t overflow the modulus.

So, we can directly take the square root of $c$ and recover $m$: cvctf{r4b1n_Cryp70_K1nd4_c0mpL1C4t3d?}

ECC Quiz

Elliptic Curve Cryptography (ECC) is a method of public-key cryptography based on the algebraic structure of elliptic curves over finite fields. Learning ECC is important for both CTFs and real-world applications. This challenge is a quiz to test your knowledge of ECC.

We’re presented with 3 challenges:

Stage 1

Curve parameters:
p = 12343
a = 592
b = 7115
Point P: (11026, 120)
Find the point Q = 6526P.

We can implement this easily with SageMath:

p = 12343
a = 592
b = 7115
E = EllipticCurve(GF(p), [a, b])
P = E(11026, 120)
print(6526P * P)

Stage 2

p = 509295886912065245778267839719131...
Point M on the curve: (2537252361667104858..., 35717165005164305678230...)
Point N on the curve: (1403327179778835458..., 15497138187228633232449...)

Substituting points $M$ and $N$ into the elliptic curve equation $y^2=x^3+ax+b$, we get a linear system of two variables that we can solve:

d1 = (M[1] ** 2 - M[0] ** 3) % p
d2 = (N[1] ** 2 - N[0] ** 3) % p
a = (d2 - d1) * pow(N[0]- M[0], -1, p) % p
b1 = (d1 - a * M[0])%p
b2 = (d2 - a * N[0])%p
assert b1 == b2
print(f'({a},{b1})')

Stage 3

p = 637846570100700166014657051461
a = 203640750416559678507746325544
b = 473633936157186352921500395381
P = (345786425541538837773613382772, 346276231851714422783705630404)
Q = uP = (21789715975353518248910995346, 551656160364627681753904141972)

This is the ECDLP problem, but here $p$ is small so we can apply built-in SageMath algorithms for finding the discrete log:

E = EllipticCurve(GF(p), [a, b])
P = E(345786425541538837773613382772, 346276231851714422783705630404)
Q = E(21789715975353518248910995346, 551656160364627681753904141972)
print(P.discrete_log(Q))

1337

A leet challenge.

P = getPrime(128)
ZmodP = Zmod(P)
a, b, c, d = flag1, flag2, flag3, flag4
x, y, z, w = ZmodP(a), ZmodP(b), ZmodP(c), ZmodP(d)

print("P:", P)
print("L:", x^1+y^3+z^3+w^7)
print("E:", y^1+z^3+w^3+x^7)
print("E:", z^1+w^3+x^3+y^7)
print("E:", w^1+x^3+y^3+z^7)
print("T:", x+y+z+w)

We’re given a system of polynomial equations in the field GF(p), where each variable is a portion of the flag. We can solve these equations cleanly with Gröbner bases in SageMath:

R.<x,y,z, w> = Integers(p)[]

f.append(x^1+y^3+z^3+w^7 - vals[0])
f.append(y^1+z^3+w^3+x^7 - vals[1])
f.append(z^1+w^3+x^3+y^7 - vals[2])
f.append(w^1+x^3+y^3+z^7 - vals[3])
f.append(x+y+z+w - vals[4])

J = R.ideal(f[0],f[1], f[2], f[3], f[4])
assert J.dimension() == 0

print(J.variety())

This SageMath thread describes the procedure in more detail.

Weird dlog

NBITS = 1337

def keygen():
    p = getPrime(NBITS)
    q = p + 2
    while not isPrime(q):
        q += 2

    n = p**2 * q
    g = getRandomRange(2, n-1)
    assert pow(g, p-1, p**2) != 1
    return (g, n), p

(g, n), pk = keygen()
print(f"g = {g}")
print(f"n = {n}")

m = pow(g, bytes_to_long(flag), n)
print(f"m = {m}")

This challenge uses the Okamoto-Uchimaya cryptosystem, though the encrypted message is simply $g^m$ rather than $g^mh^r$.

First, notice that the prime generation is weak - $p$ and $q$ will be very close to each other, and we can recover them by taking the cube root of $n$ and bruteforcing neighbouring numbers to find the primes.

guess = iroot(n, 3)[0]

for i in range(-10 ** 4, 10 ** 4):
    p = guess + i
    if isPrime(p) and n % (p) ** 2 == 0:
        q = n // (p ** 2)
        break

assert n == p ** 2 * q

Now, we can apply the decryption process described in the Okamoto-Uchimaya cryptosystem article linked above:

a = (pow(m, p-1, p**2) - 1) // p
b = (pow(g, p-1, p**2) - 1) // p
m = a * inverse(b, p) % p

print(long_to_bytes(m))

Flag: cvctf{Tatsuaki_Shigenori_uncommon_cryptosystem}

A Tale of Two Systems

It’s impossible to get a secure cryptosystem by combining two insecure cryptosystems.

This challenge is split into two stages independent from each other.

Stage 1

NBITS = 1024

def system_one(m: bytes):
    a, b = [getRandomNBitInteger(NBITS) for _ in range(2)]
    p = getPrime(2 * NBITS)
    q = getPrime(NBITS // 2)
    g = inverse(a, p) * q % p

    ct = (b * g + bytes_to_long(m)) % p

    print(f"p = {p}")
    print(f"g = {g}")
    print(f"ct = {ct}\n")

At first, this system doesn’t seem solvable because $a$ and $b$ are randomly generated and used in the encryption process. However, since we know the relative sizes of the parameters, we can apply some ✨ lattice magic ✨ to recover $a$ and $b$, and subsequently $m$.

First, the sizes of the internal variables are bounded by:

• $a$ - 1024 bits
• $b$ - 1024 bits
• $p$ - 2048 bits
• $q$ - 512 bits
• $g$ - 2048 bits
• $ct$ - 2048 bits

From the encryption process, we have that:

$$g \equiv a^{-1}q \mod p$$ $$ga \equiv q \mod p$$

Thus, there exists some integer $k$ such that $ga = pk + q$.

Since $ga$ is 3072 bits and $p$ is 2048 bits, $k$ will be around $1024$ bits.

Now, consider the lattice:

$$\begin{bmatrix} p & 1 \
g & 1 \end{bmatrix}$$

Notice that we can express the vector $(q, a-k)$ as a linear combination of the rows of the lattice:

$$(q, a-k) = a(g, 1) + -k(p, 1)$$

Since $q$ is 512 bits while $a$ and $k$ are $1024$ bits, this vector is “small” compared to the original rows with 2048 bit numbers. So, we can apply LLL to find a small basis vector:

m = Matrix([[p, 1], [g, 1]])
print(m.LLL())

Now that we have $q$ and $a$ from the lattice reduction, we can decrypt the message.

Observe that:

$$a \cdot ct \equiv abg + am \equiv (g^{-1}q)bg + am \equiv bq + am \mod p$$

However, since $p$ is 2048-bit and $bg$ and $am$ are both around ~1500 bits, $bq + am < p$. From this, recovering $m$ is easy:

$$m \equiv (bq + am)a^{-1} \mod q$$

m = Matrix([[p, 1], [g, 1]])
m = m.LLL()
q = m[0][0]
a = inverse(g, p) * q % p
temp = a * ct % p
m = temp * inverse(a, q) % q
print(long_to_bytes(m))

Flag: cvctf{n0_On3_1S_u53l355_1n_7h15_w0r1d_...

Stage 2

def system_two(m: bytes):
    p, q = [getPrime(NBITS // 2) for _ in range(2)]
    n = p * q
    e = 0x10001
    ct = pow(bytes_to_long(m), e, n)

    print(f"n = {n}")
    print(f"e = {e}")
    print(f"ct = {ct}")
    
    # what if q is reversed?
    q = int('0b' + ''.join(reversed(bin(q)[2:])), 2)
    hint = p + q - 2 * (p & q)
    print(f"hint = {hint}")

First, let’s make sense of the hint: what does x + y - 2 * (x & y) represent for two arbitrary integers $x$ and $y$?

Let’s say $a_i$ represents the $i$th bit of a number $a$. Working in binary, $(x \& y)_i$ is 1 if and only if $x_i = y_i = 1$. When we add $x$ and $y$ in those positions, the sum of $1+1$ in binary will carry over to the next position. But this is perfectly cancelled out when we subtract $(x \& y)$ shifted to the left by 1.

In other words, if $x_i = y_i = 0$ or if $x_i=y_i=1$, then the corresponding bit $(x \& y)_i$ is 0. This is just the XOR operation between $x$ and $y$!

Our goal is to factor $n$, and we currently know:

• $n = pq$
• $p \oplus rev(q)$

Similar: XORSA

A similar problem appeared in PlaidCTF, where $p \oplus q$ was given. The central idea of one solution is to find the bits of $p$ and $q$ one by one.

Starting from the lowest bit, there are always two possibilities for $(p, q)$ since we know $(p \oplus q)$. We can try both of these possibilities recursively, for a naive solution of $2^k$ where $k$ is the number of bits in $n$. But, we can prune the majority of the search space by checking that $$p_0 \cdot q_0 \equiv n \mod 2^l$$

for our current $p_0$ and $q_0$ (lower bits of $p$ and $q$). This optimization is enough to solve the XORSA challenge.

Back on track

Let’s apply a similar idea to our problem, but instead of starting only from the lower bits, we recurse over the lower and higher bits simultaneously.

Specifically, we can guess the highest bits of $rev(q)$ and the highest bits of $p$. At the same time, we can guess the lowest bits of $rev(q)$ and the lowest bits of $p$. Note that the highest bits of $rev(q)$ are the lowest bits of $q$, and vice versa.

To optimize this brute force, at each step we prune over the lower bits by checking that:

$$p_{low} \cdot q_{low} \equiv n \mod 2^l$$

Additionally, we prune over the top bits:

• If we set the remaining bits of $p_{high}$ and $q_{high}$ to $1$, the product $p_{high}q_{high}$ must be greater than $n$
• If we set the remaining bits of $p_{high}$ and $q_{high}$ to $0$, the product $p_{high}q_{high}$ must be less than $n$.

The final solve script:

n = 153342396916538105228389...
e = 65537
ct = 1073382308863262771844706024...
# p xor (reverse q)
xor = 35510848380770904338319...
NBITS = 512

# q = highQ || lowQ and p = highP || lowP, where all high/low have idx bits
def find(idx, lowP, highP, lowQ, highQ):

    if idx == NBITS:
        assert highP * highQ == n
        print("FOUND!")
        print(highP)
        print(highQ)
        exit()


    highX = (xor >> (NBITS - 1 -idx)) & 1
    lowX = (xor >> idx) & 1

    possibleLow = []
    possibleHigh = []
    
    # find possible (highP, lowQ) pairs from the MSB of the XOR
    if highX == 1:
        possibleHigh.append(((highP << 1) | 1, lowQ))
        possibleHigh.append((highP << 1, lowQ + (1 << idx)))
    else:
        possibleHigh.append((highP << 1, lowQ))
        possibleHigh.append(((highP << 1) | 1, lowQ + (1 << idx)))
    
    # find possible (lowP, highQ) pairs from the LSB of the XOR
    if lowX == 1:
        possibleLow.append((lowP, (highQ << 1) | 1))
        possibleLow.append((lowP + (1 << idx), highQ << 1))
    else:
        possibleLow.append((lowP, highQ << 1))
        possibleLow.append((lowP + (1 << idx), (highQ << 1) | 1))


    for highP, lowQ in possibleHigh:
        for lowP, highQ in possibleLow:
            # prune lower bits
            if lowP * lowQ % (1 << (idx + 1)) != n % (1 << (idx + 1)):
                continue
            
            pad = NBITS-1-idx

            # check upper bit bounds
            if (highP << pad) * (highQ << pad) > n:
                continue

            if ((highP << pad) + (1 << pad) - 1) * ((highQ << pad) + (1 << pad) - 1) < n:
                continue

            find(idx+1, lowP, highP, lowQ, highQ)

find(0, 0, 0, 0, 0)

Partial flag: _wH0_l16h73N5_tHe_BurD3nS_0F_4n07h3R.-_-}

Final flag: cvctf{n0_On3_1S_u53l355_1n_7h15_w0r1d_..._wH0_l16h73N5_tHe_BurD3nS_0F_4n07h3R.-_-}