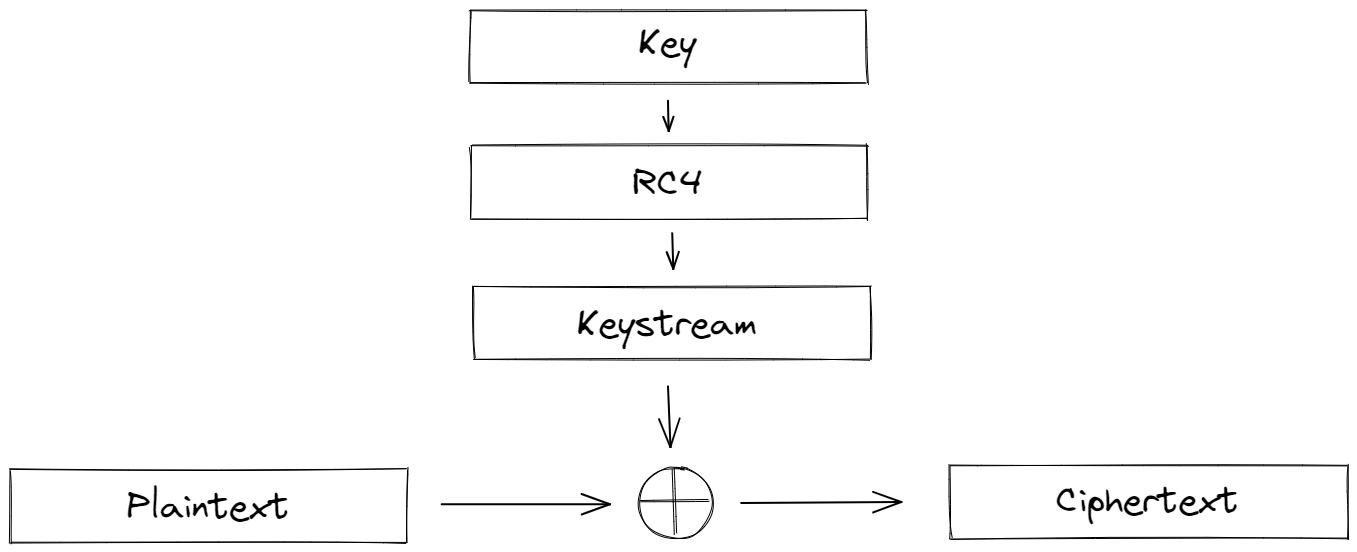
RC4

Rivest Cipher 4 (RC4) was designed by Ron Rivest and first published (or rather, leaked) in 1994. It’s considered a stream cipher, where the key generates a keystream that’s combined with the plaintext (usually through XOR $\oplus$).

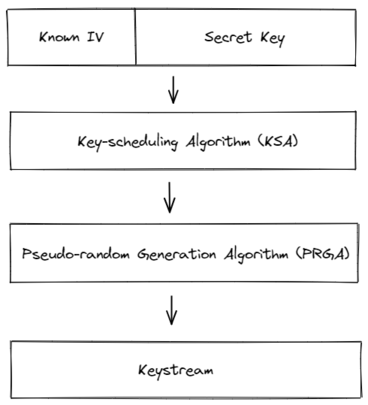
Generating the keystream is split into two steps:

• The Key-scheduling Algorithm (KSA) initializes a permutated array of all 256 bytes while mixing in the key
• The Pseudo-random Generation Algorithm (PRGA) uses the secret permutation to output one byte of the keystream at a time

Key-scheduling Algorithm (KSA)

First, the array is initialized with the identity permutation:

S = [i for i in range(256)]

Next, two pointers $i$ and $j$ permutate the array by swapping elements. The key is also mixed in during this step:

j = 0
for i in range(256):
    j = (j + S[i] + key[i % len(key)]) % 256
    S[i], S[j] = S[j], S[i]

Now, the array $S$ is permutated and kept secret.

Pseudo-random Generation Algorithm

Similar to the KSA, the PRGA also uses two pointers (which should be kept secret). A series of operations outputs a byte of the keystream at a time while also modifying the state of the array:

• Each step, $i$ is incremented and $j$ increases by $S[i]$
• The values of $S[i]$ and $S[j]$ are swapped
• A third value taken from the sum of $S[i]$ and $S[j]$ is used as the keystream byte

Here’s an implementation of the PRGA:

i = 0
j = 0
while True:
    i = (i + 1) % 256
    j = (j + S[i]) % 256
    S[i], S[j] = S[j], S[i]
    K = S[(S[i] + S[j]) % 256]
    print(K)

Finally, each keystream byte is XOR’ed with the plaintext to produce the ciphertext. Since XOR is its own inverse (that is, $A \oplus A = 0$), encryption and decryption follow the exact same process.

Putting everything together, a full implementation of RC4:

key = b'Secret'
plaintext = b'Attack at dawn'

S = [i for i in range(256)]

j = 0
for i in range(256):
    j = (j + S[i] + key[i % len(key)]) % 256
    S[i], S[j] = S[j], S[i]

i = 0
j = 0
keystream = []
for i in range(len(plaintext)):
    i = (i + 1) % 256
    j = (j + S[i]) % 256
    S[i], S[j] = S[j], S[i]
    K = S[(S[i] + S[j]) % 256]
    keystream.append(K)

ciphertext = [x ^ y for x, y in zip(plaintext, keystream)]
print(''.join([hex(c)[2:].zfill(2) for c in ciphertext]))

Fluhrer, Mantin, and Shamir attack

Often, the key fed into the KSA is made up of a known IV and a secret key. If they’re concatenated together, then the Fluhrer, Mantin, and Shamir attack can recover the original key through weak IVs (given that we know the first byte of all keystreams).

The simplest weak IVs are made up of 3 bytes in the form $(A+3, N-1, X)$, where we know the first $A$ words of the secret key, $N$ is 256, and $X$ is any number.

To find the next byte of the secret key, we first run $A+3$ iterations of the Key-scheduling Algorithm to permutate the array $S$. Notice that the first $A+3$ values of the entire key (IV concatenated with secret key) are known to us.

I’ll skip over the specifics of how the weak IV works; what’s important is that in the end, the $i$ and $j$ pointers advance, swapping elements in such a way so that we can recover the next key byte through the equation:

$$Key[i] \equiv (O - j - S[i]) \mod 256.$$

Here, $O$ is the first byte of the keystream, while $i$ and $j$ are the pointers from the KSA iterations. The equation above holds true with 5% probability, which is easily distinguishable from a random byte. With 60 different values of $X$, we have over a 50% chance of recovering the next byte of the key.

In summary, we can recover the secret key with high probability if it’s directly appended to a known weak IV and we know the first bytes of the keystreams.

Fluhrer, Mantin, and Shamir attack in code:

# Implementation of RC4 encryption (only returns the keystream)
def encrypt(IV):
    key = IV + b'Vulnerable Secret Key'
    S = [i for i in range(256)]

    j = 0
    for i in range(256):
        j = (j + S[i] + key[i % len(key)]) % 256
        S[i], S[j] = S[j], S[i]
    
    i = 0
    j = 0
    keystream = []

    #  In reality we only need the first byte of the keystream; 64 is an arbitrary choice
    for i in range(64):
        i = (i + 1) % 256
        j = (j + S[i]) % 256
        S[i], S[j] = S[j], S[i]
        K = S[(S[i] + S[j]) % 256]
        keystream.append(K)

    return keystream

A = 0
curKey = b''

while True:
    results = []
    for x in range(256):
        # Construct weak IVS
        IV = bytes([A + 3, 255, x])
        keystream = encrypt(IV)
        knownKey = IV + curKey

        # Run KSA iterations with known key bytes
        S = [i for i in range(256)]
        j = 0
        for i in range(A + 3):
            j = (j + S[i] + knownKey[i % len(knownKey)]) % 256
            S[i], S[j] = S[j], S[i]
        i += 1
        # Store the most likely next key byte
        results.append((keystream[0] - j - S[i]) % 256)

    # Next byte of the key should be the most common one
    nextByte = max(set(results), key = results.count)
    curKey += bytes([nextByte])
    print(f'Current Key: {curKey}')

    # Repeat for the next byte
    A += 1